Matemáticas Administrativas, resumen de la unidad 1

Un desconocimiento común en muchos empresarios consiste en no utilizar las herramientas que les brindan las matemáticas administrativas, para calcular las funciones de costo, ingreso y utilidad.
+	→	Por lo tanto, no toman decisiones con base en cálculos previos de costo-beneficio, sino de manera empírica, lo que impide visualizar estrategias integrales que se anticipen a los hechos.
Deben anticipar los efectos generados por las variaciones de diversos factores (llamados variables) que intervienen en los sucesos y/o eventos del entorno de los negocios. Estas variables se pueden plasmar en una expresión matemática llamada función, misma que relaciona el efecto (Y) que es generado por diversas causas (x1, x2…..xn).

Las matemáticas administrativas ofrecen al empresario la posibilidad de responder preguntas importantes como:
  ►¿Cuál será mi utilidad por la producción de X piezas?
  ►¿Cuál será el costo de producir X piezas?
  ►¿Cuál es el número de piezas que debo producir para no tener pérdidas en mi empresa?
Aunque la respuesta se puede considerar tan simple como un número, los números se obtienen a través de números.

Introducción

Las matemáticas es una herramienta que permite verificar, mediante modelos gráfico-numéricos, los efectos que pueden generar variaciones de los elementos o factores que intervienen en los fenómenos y sucesos que se presentan a lo largo de nuestra vida.

Funciones y variables                                                                              

La relación funcional o función ayuda a describir de manera práctica situaciones presentes en la vida en las que un valor o cantidad que varía, depende de la función o determina el valor de otra, por ejemplo:

►La cantidad de impuestos que paga una persona o empresa depende de los ingresos de ésta.
Las matemáticas se encuentran en la vida cotidiana y las funciones se usan hasta en la más mínima acción.

De ahí se observa que se pueden tener variables o valores que dependen o cambian cuando un valor determinante varía. Otro ejemplo representativo es el puntaje obtenido en un juego de tiro al blanco, en el que hay dibujados en un tablero 5 círculos concéntricos y en cada uno se pueden tener los siguientes valores: 5, 10, 15, 20, 25, iniciando desde el exterior hasta el centro del tablero, como se muestra:
La máxima puntuación se obtiene atinándole al círculo que queda en el centro del tablero (25 puntos), y disminuye conforme se aleja hacia la orilla, así se obtienen dos conjuntos, uno correspondiente a los círculos y que se definirá como el conjunto C, y el otro correspondiente a la puntuación y que se llamará P, esto es:

C = {1, 2, 3, 4, 5}
P = {5, 10, 15, 20, 25}

Ambos conjuntos están relacionados entre sí, ambos dependen el uno del otro y se puede representar mediante una tabulación o una gráfica.

Tabla de puntuación
Círculo	Puntuación
1	5
2	10
3	15
4	20
5	25

En ambas representaciones se puede comprobar que para cada elemento del conjunto P (puntuación) hay sólo un valor o elemento que le corresponde del conjunto C (círculo), es decir, que se cuenta con las siguientes parejas ordenadas:

(1, 5), (2, 10), (3, 15), (4, 20), (5, 25).

Otra forma de representación es mediante un modelo matemático (considerando los datos del ejemplo anterior) es que si se acierta en el círculo del centro se tendrán 25 puntos y en el círculo más alejado del centro se obtendrán 5 puntos, así se observa que existe una situación de dependencia: el puntaje dependerá a qué círculo del tablero se acierte y cada acierto tiene un valor que resulta de multiplicar el número del círculo al que se acierta por cinco.

Función: Y=5X
Variable dependiente: Y
Variable independiente: X

Para llevar a cabo esta operación es necesario conocer el número de círculo al que se acierta, por lo que el número de círculo es el valor que alimenta al modelo matemático, es decir, son los valores de entrada a los que hay que multiplicar por cinco, para que dé el resultado del puntaje obtenido, lo que dará los valores de salida, si se utilizan además variables que permitan identificar a cada uno de los valores, es decir y para el puntaje y x para los círculos, podremos obtener la siguiente expresión:

y=5x	En donde y corresponde a una variable dependiente y x a una variable independiente, que conforman lo que se conoce como función.

Material de apoyo:
http://www.eduteka.org/MI/master/interactivate/index.php

Conceptos relacionados a las funciones variables dependientes e independientes.

Función	Variable Dependiente	Variable Independiente
Es la correspondencia entre dos conjuntos: uno de valores de entrada y otro de valores de salida, en donde existe una regla de operación que determina para cada valor de entrada un solo valor de salida.	Es aquella cuyo valor, propiedad o característica se trata de cambiar mediante la manipulación de la variable independiente.	Es aquella que es manipulada en un experimento o evento con el objeto de estudiar como incide sobre la variable dependiente, esto significa que las variaciones en la variable independiente repercutirán en variaciones en la variable dependiente.

A continuación, se muestran los  nombres de las partes de una función; se utiliza la expresión matemática:

Esta expresión, completa, relaciona una variable independiente con una variable dependiente.

La “y” es la llamada variable dependiente, pues su valor dependerá de los valores que asignemos a la variable “x”. Por ejemplo, si decidimos dar un valor de
la “y” tomará un valor:
Para cada valor quedemos a “x”, “y” tomará a su vez un valor. Por lo tanto, la “x” es lo que conocemos como variable independiente, pues el valor que toma no depende de ninguna otra variable y podemos decidirlo. La expresión completa que contiene a ambas variables, es lo que llamaremos función.

Tipos de  funciones y su aplicación

Como se vio en el tema anterior, la función es la correspondencia de las variables dependientes e independientes, y a partir de las expresiones algebraicas, existen diferentes tipos de funciones, las cuales se verán a continuación.

Función constante

Es aquella que tiene la forma :

f(x)=c

En donde c es un número real.


Ejemplo:
Sea f(x)=10, debido a la forma de la función, a la variable "x" se le puede asignar cualquier valor que se desee, sin embargo, el resultado de la función será siempre 10.

x	f(x)=10	Pares ordenados	Gráfica
-15	10	(-15,10)
-10	10	(-10,10)
-5	10	(-5,10)
0	10	( 0,10)
5	10	( 5,10)
10	10	(10,10)
15	10	(15,10)

Observa la gráfica que se obtiene a partir de la tabla, se presenta una recta paralela al eje de las "x" (abscisas) y que f(x)=10, corta el eje de las Y (ordenadas) en el punto (0,10)

En este caso, la "x" toma los siguientes valores: -15, -10, -5, 0, 5, 10, 15.

La variable independiente toma siempre el mismo valor (la función es constante e indica que y=10). Se forman entonces siete pares ordenados (x,y), que son: (-15, 10), (-10, 10), (-5, 10), (0, 10), (5, 10), (10, 10), (15, 10). Hay que recordar que la variable independiente, "x" puede tomar valores no enteros, por lo que existe una infinidad de pares ordenados aunque no se encuentren expresados en la tabla que se presenta. La gráfica es una línea recta horizontal (paralela al eje de las x), que como la función lo indica, pasa por (0, 10). Esta gráfica nos muestra cómo luce una función lineal.

Tipos de  funciones y sus gráficas

Función lineal

Una función lineal tiene la forma:

f(x)=mx+b

Una función f es lineal sí y sólo sí f(x) puede ser escrita en la forma f(x)= mx + b, en donde a y b son constantes y a≠0
En donde:
m y b son cualquier número real y además m≠0
m=pendiente de la recta.
Si m>0, conforme los valores de "x" aumentan también lo hacen los de "y"
Si m<0, conforme los valores de "x" aumentan los valores de "y" disminuyen.
b= ordenada al origen (punto donde la recta corta el eje de las ordenadas).

Suponga que f(x) = mx+b es una función lineal y que y = f(x). Entonces y=mx+b, la cual es una ecuación de recta con pendiente m y b es la intersección con el eje y. Así, la gráfica de una función lineal es una recta. Decimos que la función f(x)=mx+b tiene pendiente m.¹
¹http://moodle2.unid.edu.mx/dts_cursos_mdl/lic/AE/MU/S08/MU08_Lectura.pdf

Ejemplo:
Sea f(x)=2x+4, se observa que se trata de una función lineal en donde:
m = 2
b = 4
es decir, que cuando x = 0, f(x) = y = 4.

Observa la siguiente representación gráfica:

x	f(x)=10	Pares ordenados	Gráfica
-3	-2	(-3,-2)
-2	0	(-2,0)
-1	2	(-1,2)
0	4	( 0,4)
1	6	( 1,6)
2	8	(2,8)
3	10	(3,10)

Así, se observa que la gráfica es una línea recta creciente, esto se debe a que m > 0, por lo que conforme “x” aumenta, también lo hace ”y”, por lo tanto, se trata de una función creciente.

En este caso, la x toma los siguientes valores: -3, -2, -1, 0, 1, 2, 3. La variable dependiente toma valores que dependen efectivamente de la variable independiente.

Por ejemplo
para x=-3, y = 2(-3)+4 =-6+4 =-2.
Para x=-2, y = 2(-2)+4 =-4+4 = 0
Para x=-1, y = 2(-1)+4 =-2+4 = 2
Para x= 0, y = 2 (0)+4 = 0+4 = 4
Para x= 1, y = 2 (1)+4 = 2+4 = 6
Para x= 2, y = 2 (2)+4 = 4+4 = 8
Para x= 3, y = 2 (3)+4 = 6+4 = 10

Función cuadrática

Una función cuadrática se describe como una función polinomial de grado dos o ecuación de segundo grado.²
²http://moodle2.unid.edu.mx/dts_cursos_mdl/lic/AE/MU/S09/MU09_Lectura.pdf
Una función f es una función cuadrática si y sólo si f(x) puede ser escrita en la forma f(x) = ax²+bx+c, donde a, b y c son constantes y a≠0.

Una función cuadrática es aquella que tiene la forma:

f(x)=ax²+bx+c

Donde a, b y c son números reales, mientras que b y c pueden valer cero.

La forma de la gráfica de una función cuadrática es una parábola (que es el nombre que recibe la gráfica de la función cuadrática), en donde el vértice es el punto más bajo si la parábola abre hacia arriba y el vértice es el punto más alto cuando la parábola abre hacia abajo.


Si a >0, la parábola abre hacia arriba. Si a<0, la parábola abre hacia abajo. El vértice está dado por las coordenadas V(xv,yv) que se calcula con las siguientes fórmulas:

xv=-b yv=4ac-b²
     2a         4a

Ejemplo en:
http://contenidosdigitales.ulp.edu.ar/exe/matematica3/ejemplos_resueltos2.html

Hay que recordar que las variables “x” e “y”, pueden tomar valores no enteros, por lo que existe una infinidad de pares ordenados aunque no se encuentren expresados en la tabla que se presenta.

Función Polinominal

Son, como su nombre lo dice, funciones que constan de un polinomio.
Una función es polinominal si:
El valor de "n" determina el grado de la función polinomial, que puede ser lineal, cuadrática, cúbica, de cuarto grado, de quinto grado, etc., dependiendo del valor de "n", es decir, el valor más alto del exponente de la función es el que determinará de qué grado es la función.
"n" es un entero positivo, llamado, grado del polinomio. Resulta evidente, que el coeficiente del grado mayor, no puede ser cero, o sea, "a" tiene que ser diferente de cero, para que el grado del polinomio sea "n". Cualquiera de los otros coeficientes puede ser cero.


Ejemplos de funciones polinómicas son:
f(x)=¼x³+3x²-5x+3 (Función de tercer grado, ya que el exponente mayor es 3)
f(x)=x²+2x+3, (Función polinómica de segundo grado, o sea cuadrática, cuya gráfica es una parábola)
f(x)=(x-1)(x-2)(x+1)(x-3)(x+2)(x) de sexto grado, al multiplicar todos los paréntesis, nos daría como mayor exponente el 6. Esta función se grafica más adelante, para hacer notar, que las intersecciones con los ejes y la factorización de la función polinomial tienen una estrecha relación.

La gráfica de las funciones polinómicas depende del grado de la función. Las funciones polinómicas de ciertos grados tienen ciertas alternativas de gráfica.

Una función polinómica con el más alto número de intersecciones con el eje "x" permisible, es aquella que se puede determinar su gráfica y su ecuación.
Una función de, por ejemplo, tercer grado puede tener como máximo 3 intersecciones con el eje "x".
Una función de sexto grado puede tener como máximo 6 intersecciones con el eje "x".

Cabe aclarar, que las funciones polinómicas, aunque no conozcamos ahora los términos específcos, son funciones continuas,sin asíntotas verticales, ni horizontales, que según el grado pueden presentar máximos, mínimos y puntos de inflexión.

Suponiendo que la función que se nos presenta es de tercer grado, y sus intersecciones están en x =2, x = -1 y en x = -3; la ecuación de la función es f(x)=(x-2)(x+1)(x+3)

Debe quedar claro, que se tiene que conocer el grado de la función polinómica, ya que sin éste, las conclusiones que se puedan sacar pueden estar equivocadas. Tenemos una función polinómica de grado 6, que sus intersecciones se encuentran en x=1, x=2, x=-1, x= 3, x=-2 y en x= 0; por lo tanto la función es: f(x) = (x-1)(x-2)(x+1)(x-3)(x+2)(x)

http://bibliotk.gdl.up.mx/calculo/polinomicas.html

Función racional

Una función racional "h(x)" es una función que puede escribirse como cociente de dos polinomios f(x) y g(x) donde f(x) y g(x) son funciones polinominales y g(x) es una función diferente de cero; es decir: g(x)≠0

h(x)=fx
       gx

Por ejemplo:

f(x)=3
      x-2

g(x)=5x-3
       x²-4

Características que las diferencian de las funciones polinómicas
-Singularidades:En algunos casos, algunos valores de "x" son problemáticos. Esto debido, a que en las funciones racionales hay un denominador que puede ser 0 y no podemos dividir entre 0. Esos valores de "x" que hacen 0 el denominador, juegan un papel especial. Como no podemos calcular el valor de la función en esos valores decimos que la función no está definida para esos valores de "x".
También decimos que esos puntos no pertenecen al dominio de la función. El dominio de una función racional está determinado por restricciones impuestas por el denominador: dividir entre 0 es imposible.
El dominio es el conjunto de los números reales para los que la función está definida. En el caso de las funciones racionales es el conjunto de todos los números reales que no son ceros del denominador. Por lo tanto, para determinar el dominio de una función racional tenemos que encontrar los ceros reales del denominador.
A estos puntos se les llama singularidades y es interesante ver cómo se comporta la función cerca de esos puntos.
-Puntos de corte con el eje de abcisas: Se trata de encontrar los valores de "x" que hacen que el gráfico de la función cruce el eje de abcisas. Son los valores de "x" para los que f(x)=0.
-Continuidad: Las funciones racionales son continuas en su dominio (pero su dominio puede no ser todos los números reales).
-Comportamiento "en el infinito": Es interesante el estudio del comportamiento de la función cuando "x" se hace más y más grande en valor absoluto (siendo "x" positivo o negativo). Veremos que en algunos casos la función se aproxima a una recta (horizontal u oblicua). En estos casos diremos que la función tiene una asíntota horizontal u oblicua (según los casos). En todos los casos el comportamiento de una función racional "en el infinito" está determinado por una función polinómica.

http://www.matematicasvisuales.com/html/analisis/rational/rational1.html

Gráfica de una función racional
Para elaborar una gráfica de una función racional, primero debemos desarrollar una tabla de valores y posteriormente se representan en un sistema de coordenadas.
http://portalacademico.cch.unam.mx/alumno/aprende/matematicas4/funcionesracionales

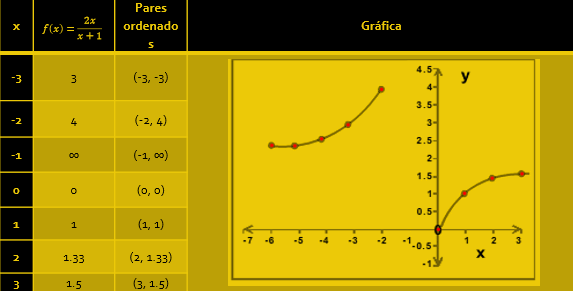
Ejemplo: Sea
f(x)=2x
      x+1
En la siguiente gráfica se observa que en -1 la función crece al infinito ∞
Una función exponencial es aquella en la que la variable independiente se encuentra como exponente de un número constante:

f(x)=aˣ

La gráfica es creciente cuando a>1 y decreciente cuando 0< a < 1
Ejemplo: Sea f(x)=2ˣ

x	f(x)=2ˣ	Pares ordenados	Gráfica
-2	0.25	(-2,0.25)
-1	0.5	(-1,0.5)
0	1	( 0,1)
1	2	( 1,2)
2	4	(2,4)
3	8	(3,8)

En este caso, la x toma de los siguientes valores:  2,-1,0,1,2,3. La variable dependiente toma valores que dependen efectivamente de la variable independiente.

Por ejemplo
Para  x=-2→y=2⁻²=1/2²=¼=0.25
Para  x=-1→y=2⁻¹=1/2¹=½=0.5
Para x= 0 →y=2⁰=1
Para x= 1 →y=2¹=2
Para x= 2 →y=2²=4
Para x= 3 →y=2³=8

Se forman entonces 6 pares ordenados (x, y), que son: (-2, 0.25), (-1, 0.5), (0, 1), (1, 2), (2, 4), (3, 8). Hay que recordar que las variables “x” e “y”, pueden tomar valores no enteros, por lo que existe una infinidad de pares ordenados aunque no se encuentren expresados en la tabla que se presenta. La gráfica anterior nos muestra cómo luce una función exponencial.

Función logarítmica

Una función logarítmica se define como la inversa de la exponencial y puede ser representada de la siguiente manera:
a) La función del logaritmo de base "b" se define como: f(x)=log2 y=x si y sólo si y=bˣ
b) La función del logaritmo natural "e"  se define como: f(x)=lny=x si y sólo si y=eˣ
   Donde e=2.7182881828

Ejemplo: f(x)=log2ˣ
Observa la siguiente representación gráfica:

x	f(x)=log2ˣ	Pares ordenados	Gráfica
0,125	-3	(0,125,-3)
0,25	-2	(0.25,-2)
0,5	-1	(0.5,-1)
0	1	( 1,0)
1	2	( 2,1)
4	2	(4,2)
8	3	(8,3)

En este caso, la x forma de los siguientes valores: 0.125, 0.25, 0.5, 0, 1, 4, 8. La variable dependiente toma valores que dependen efectivamente de la variable independiente.

Por ejemplo
para x=0.25 →y=log₂0.25=log₂¼=log₂1/2²=log₂2⁻²=-2
para x=0.5—→y=log₂0.5=log₂½=log₂1/2¹=log₂2⁻¹=-1
para x=1——→y=log₂1=log₂2⁰=0
para x=2——→y=log₂2=log₂2¹=1
para x=4——→y=log₂4=log₂2²=2
para x=8——→y=log₂8=log₂2³=2

Se forman entonces 7 pares ordenados (x, y), que son: (0.125, -3) (0.25, -2), (0.5, -1), (1, 0), (2,1), (4,2), (8, 3). Hay que recordar que las variables “x” e “y” pueden tomar valores no enteros, por lo que existe una infinidad de pares ordenados aunque no se encuentren expresados en la tabla que se presenta. La gráfica anterior nos muestra cómo luce una función logarítmica.

Como puedes ver, cada una de las funciones tiene una representación gráfica que puede mostrar el comportamiento de una actividad o fenómeno en cualquier ámbito de tu vida.

Ingreso, costo, utilidad y punto de equilibrio

Relacionado con la administración, es importante que conozcas y sepas aplicar las funciones matemáticas, ya que en algún momento de tu vida laboral te encontrarás con ellas.

Ejemplo: Un punto de equilibrio es usado comúnmente en las empresas u organizaciones para determinar la rentabilidad de vender "X" producto.

Se te invita a estudiar los siguientes conceptos:

Ingreso

La función de ingreso total se define como: i(x)=xp
Donde:
x=número e artículos vendidos.
p=precio de venta unitario.

Es importante mencionar que la función de ingresos también puede seguir cualquier otro comportamiento algebraico: cuadrático, lineal, exponencial, entre otros.

Ejemplo:
Un club social que cuenta con 2300 afiliados está por incrementar a los asociados las cuotas mensuales, quienes actualmente pagan $500.00. Sin embargo, antes de realizar dicha operación, el consejo directivo realizó una encuesta con la que determinó que por cada incremento de $50.00 podrían perder a 15 socios.
¿Cuál será el comportamiento del ingreso del club al incrementar en $50.00 la cuota mensual?

Si se considera determinar el ingreso mensual en función de la cuota (precio) que paga cada socio, se tienen las siguientes variables:
x = nueva cuota
y = número de socios
y1 = número de socios antes del incremento en la cuota
y2 = número de socios después del incremento en la cuota

1.- El número de socios nuevos es:
y = y1–y2 =2300–(8x–3200)=5500– 8x
2.- Tomando en cuenta la función general de ingreso:
𝐼(x)=xp
𝐼(𝑥) = 𝑥 5500 − 8𝑥

Costo

La función de costo total se define como:
C(x)= Costo  variable por unidad "x" + Costos Fijos
C(x)= ax(número de artículos vendidos o producidos)+cf(costo fijo de producción)

Ejemplo:
Una maquiladora de pantalones de mezclilla ha calculado que sus costos fijos mensuales son de  $125,000.00 y que cada pantalón le genera un costo de $35.00. Para determinar el costo total de fabricación en el siguiente mes si se van a elaborar 1500 pantalones de mezclilla.

Solución: Lo primero que se deberá determinar es la función de costo total.

C(x)=ax+Cf

Donde:
C(x) =  función de costo.
x = 1500 pantalones de mezclilla.
a = costo de elaboración de un pantalón que es $35.
Cf= representa los costos fijos mensuales con un valor de $125,000.

Sustituyendo en la función de costo total se tiene: C(x)=35x+125,000 pesos.
El costo de producción de 1500 pantalones del siguiente mes será de:
C(1500)=35(1500)+125000
C(1500)=$177,500


Costo promedio o costo medio
Está relacionado con el costo total C(x) de producción o venta de "x" artículos o servicios y se obtiene al dividir el costo total de entre el número de unidades producidas o servicios ofertados:

Cm(x)=C(x)
            x
Donde:
C(x) = función de costo
x = número de artículos o servicios

Ejemplo:
El costo total de producir "x" libretas escolares por semana sigue el comportamiento de la siguiente función cuadrática:
𝐶 𝑥 = 0.63𝑥2 + 233𝑥 + $250
¿Cuál será el costo promedio de producir 10,000 unidades mensualmente, considerando que el mes tiene cuatro semanas?

Debemos determinar la función de costo promedio dividiendo la función de costo entre x:

Sustituyendo el número de libretas que se desea producir: x=10000, se tiene que:
𝐶 10000 𝑚 = 4 (6533.025)
𝑪 𝟏𝟎𝟎𝟎𝟎 𝒎 = $𝟐𝟔𝟏𝟑𝟐.𝟏

Utilidad

Se obtiene restando los costos de los ingresos:
U(x)= I(x)-C(x)

Ejemplo:
Un fabricante de cremas faciales, mensualmente tiene costos de producción de $15,000.00 y el costo de fabricación por crema es de  $4.50. Si cada crema la vende por mayoreo a las tiendas departamentales en $25.00, determine las utilidades que genera en su empresa la venta de cremas faciales si mensualmente vende en exclusiva 2000 cremas a una cadena de SPA.

Solución: si se sabe que las utilidades están representadas por:
U(x) =I(x) - C(x)

Es necesario determinar tanto la función de ingresos como la de costo total, de ahí que en este caso se tienen los siguientes datos:
x = número de cremas
𝐶𝑓= $15,000.00
𝐶𝑣= 4.50x
Cremas vendidas por mes=2000
p = $25.00

Entonces para los ingresos:
𝐼𝑥=𝑥𝑝

Sustituyendo los datos del problema:
𝑰𝒙=𝟐𝟓𝒙

Y los costos estarán dados por:
𝐶𝑥=𝐶𝑣+𝐶𝑓

Sustituyendo los datos del problema:
𝑪𝒙=𝟒.𝟓𝟎𝒙+𝟏𝟓𝟎𝟎C(x) = 4.5x + 15000

Así sustituyendo en la función de utilidad:
𝑈(𝑥)=𝐼(𝑥)−𝐶(𝑥)
𝑈(𝑥)=25𝑥−(4.50𝑥+15000)
𝑈(𝑥)=25𝑥−4.50𝑥−15000
𝑼𝒙=𝟐𝟎.𝟓𝒙−𝟏𝟓𝟎𝟎𝟎 𝒑𝒆𝒔𝒐𝒔

Si mensualmente vende 2000 cremas faciales:

𝑈200=20.5(2000 −15000
𝑈200=41000−15000
𝑼𝟐𝟎𝟎=𝟐𝟔𝟎𝟎𝟎𝒑𝒆𝒔𝒐𝒔

Por lo que mensualmente la crema facial le genera utilidades de 26,000 pesos

Punto de equilibrio

Punto de equilibrio: es el punto en que el importe de las ventas de una empresa es igual al de los costos y gastos que dichas ventas originan.

𝑰𝒙=𝑪(𝒙)

Consideraciones
Si el costo total de producción supera a los ingresos que se obtienen por las ventas de los objetos producidos o servicios vendidos, la empresa sufre una pérdida.
Si los ingresos superan a los costos, se obtiene una utilidad o ganancia.
Si los ingresos logrados por las ventas igualan a los costos de producción, se dice que el negocio está en el punto de equilibrio o de beneficio cero.

Gráficamente, el punto de equilibrio es el que está representado por la intersección de las rectas que representan a la función de costos e ingresos.

Si I(x) < C(x), entonces la empresa tiene pérdidas.
Si I(x) = C(x) la empresa no gana ni pierde, está en el punto de equilibrio.
Si I(x) > C(x) la empresa tiene ganancias.

Cierre de la unidad

En esta unidad analizaste los tipos de funciones y las operaciones que puede haber entre ellas.
El estudio de estas expresiones algebraicas te permitirá dar solución práctica a los diversos problemas que se presentan en el área económico-administrativa, a través del análisis de situaciones de optimización, costo total, ingreso, oferta y demanda, y mediante el uso de los diferentes tipos de funciones y modelos gráficos.

Se ha seleccionado una serie de recursos en línea con el fin de ofrecerte un panorama general de la unidad y alternativas en caso de que se te dificulte la comprensión de algún concepto o proceso.

Si deseas saber más de estos temas se te sugiere revisar las siguientes ligas:

Nota: Para algunas páginas deberás tener instalado el software Java para visualizar la información y realizar actividades.

Eduteka:
http://www.eduteka.org/MI/master/interactivate/index.php

Universidad Nacional de la Patagonia San Juan Bosco (s.f.). Curso de apoyo en Matemática:
http://www.ing.unp.edu.ar/matematica/images/materiales/Modulo_Ingreso.pdf

Sociedad andaluza de educación matemática THALES. Función cuadrática:
http://thales.cica.es/rd/Recursos/rd99/ed99-0416-02/indice.htm

Descartes. Elementos de una función: http://descartes.cnice.mec.es/materiales_didacticos/Funciones_formas_de_expresar/elementos.htm

Cómo calcular una utilidad marginal:
http://es.wikihow.com/calcular-la-utilidad-marginal
http://dianita-utilidadmarginal.blogspot.mx/2011/10/formula-para-calcular-la-utilidad.html

Bibliografía básica:
Chiang. (2006). Métodos fundamentales en economía matemática. (4°edición). México: Editorial McGraw-Hill.

Cissell, R., Cissell, H. y Flaspohler, D. C. (1999). Matemáticas Financieras. (2ª edición). México: Editorial CECSA.

García, E. (1998). Matemáticas Financieras por medio de Algoritmos, Calculadora Financiera y PC. México: Editorial McGraw-Hill.

Harshbarger, R. J. y Reynolds, J. J. (2005). Matemáticas Aplicadas a la Administración, Economía y Ciencias Sociales. (7°edición). México: McGraw-Hill.

Leithold, L. (2006). El cálculo. (7ª edición). Oxford: Editorial Cúspide.

Motoyuki, A. (2000). Matemáticas Financieras. Córdoba, Argentina: Despeignes Editora.

Render, B., Stair, R. M. y Hanna, M. E. (2006). Métodos cuantitativos para los negocios.México: Pearson Educación.

Spiegel, M. R. (1994). Manual de Fórmulas y Tablas Matemáticas. México: McGraw-Hill.

Thomas. (2006). Cálculo de una variable. Editorial Prentice Hall.

Toledano y Castillo, M. A. y Himmelstinede Chavarria, L. E. (1984). Matemáticas Financieras. México: Editorial CECSA.

Vidaurri, H. M. (2001). Matemáticas Financieras. (2ª edición). México: Ediciones Contables, Administrativas y Fiscales -ThomposnLearning.

Tutorial para graficar en Excel